
Fraktale można dostrzec wszędzie – na płótnach van Gogha i Pollocka, w architekturze świątyni Angkor Wat i weneckiego Pałacu Dożów, w partyturach Mozarta.
W latach 90. rozgorzała dyskusja wokół obrazów Jacksona Pollocka. Wszystko zaczęło się od tego, że pani Teri Horton kupiła za pięć dolarów obraz, o którego oryginalność spierali się znawcy sztuki. Po wielu badaniach okazało się, że płótno zostało namalowane w za ciemnej gamie, farbami akrylowymi, których Pollock nie używał, i na standardowym formacie, podczas gdy reszta jego dzieł była ręcznie docinana z płótna żaglowego.
Nadal jednak nie uznawano ekspertyz. Matematyk Richard Taylor postanowił więc jednoznacznie stwierdzić autentyczność dzieła. Za wzór wziął obraz Numer 1 z 1948 r. Wykorzystał w tym celu metodę box-countingu, która polega na nakładaniu na płótno kolejnych, coraz drobniejszych, kwadratowych siatek. Następnie zlicza się, ile kwadratów zawiera elementy obrazu. Sprawdzane jest więc, w jakim stopniu wzór pokrywa płaszczyznę.
Liczba zliczonych kwadratów jest więc miarą zajętej przez obraz powierzchni. Wartość ta oczywiście będzie się zmieniać wraz ze zmianą rozmiaru kratki. Kluczowa jest szybkość tych zmian – pozwala ona określić, ile wymiarów ma mierzony obiekt. Oto prosty przykład:
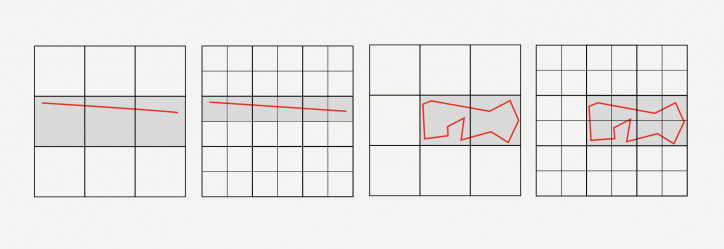
Na pierwszym rysunku znajduje się jednowymiarowa linia. Zajmuje ona trzy kratki. Co będzie, gdy zmniejszy się







